Vastgoedontwikkeling en netto contante waarde
Het ontwikkelen van vastgoed in de vorm van een project wordt steeds competitiever. Dat merk ik vrijwel dagelijks bij de implementatie van ons pakket voor vastgoedontwikkelaars Invantive Estate. Het is belangrijk om projecten onderling goed te vergelijken op onder andere hun bijdrage aan het resultaat. Bijvoorbeeld op basis van netto contante waarde (afgekort als “NCW”).
Andere woorden voor netto contante waarde zijn “Netto Huidige Waarde” (afgekort “NHW”) of “Netto Actuele Waarde” (afgekort “NAW”). Het Engele woord voor “netto contante waarde” is “Net Present Value”, vaak afgekort als “NPV”. De termen worden door elkaar gebruikt.
De netto contante waarde is de waarde van een reeks (samenhangende) geldstromen. Echter, bij de bepaling van de netto contante waarde wordt niet elke Euro even zwaar gewogen. De weging is afhankelijk wanneer in de toekomst de kasstroom plaatsvindt. Dat is vergelijkbaar met geld lenen en terugbetalen: je leent liever geld aan een vriend als hij eerst datzelfde bedrag aan jou geeft in plaats van dat jij eerst geld geeft en hij over 100 jaar terugbetaalt.
Geld dat snel ter beschikking staat weegt zwaarder positief dan wanneer het later binnenkomt. En geld dat eerder wordt uitgegeven weegt zwaarder negatief dan wanneer het later uitgegeven wordt. De weging gaat op basis van een percentage. Dit percentage wordt extern bepaald, bijvoorbeeld door de kosten van geld en risico. In de rest van de tekst wordt dit verder uitgelegd.
Je kunt op basis van de netto contante waarde de vastgoedprojecten selecteren waar je het beste resultaat mee kunt behalen.
In deze blog komen een aantal relevante basisbegrippen uit de financiële rekenkunde voorbij. Deze basisbegrippen zijn nuttig voor vastgoedontwikkelaars, omdat ze vooral bij complexere projecten helpen te bepalen of een ontwikkelingsproject voldoet aan de rendementseisen van de organisatie. De uitleg is gebaseerd op materiaal van Scalar. Bij Scalar heb ik zelf ook de fijne kneepjes van het vastgoed rekenen mogen leren. Bij deze wil ik hen dan ook bedanken voor het ter beschikking stellen van dit materiaal. Regelmatig organiseert Scalar cursussen waarin verder ingegaan wordt op rekenen aan vastgoedprojecten. Onderwerpen zoals “residuele grondwaarde” en “onrendabele top” komen dan ook aan de orde.
Monte Carlo simulaties
Kasstroom prognoses en omzet prognoses kun je met een paar muisklikken massaal doorrekenen in Invantive Estate, op basis van de huidige prognose einde werk. Een statistisch onderzoek geeft je nog meer inzicht in de kans dat het uiteindelijke resultaat ver afwijkt van het geprognosticeerd resultaat, bijvoorbeeld op basis van Monte Carlo simulaties. In deze blog ga ik niet in op dit soort waarderingsmodellen. Dergelijke statistische onderzoeken met Monte Carlo simulaties kun je doen nadat je met Microsoft Excel en Invantive Control een rekenmodel hebt opgezet en ingevuld voor een plangebied.
Kasstroom(schema)
Stel dat je € 100,- op een spaarrekening stort tegen een rentevergoeding van 10% per jaar. De bank zal dan na 1 jaar € 10,- rente bijschrijven op je rekening. Je kunt na 1 jaar dus € 110,- opnemen. In onderstaand figuur is dit grafisch weergegeven.
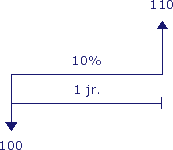
Deze grafische weergave wordt in de financiële rekenkunde een “kasstroomschema” (Engels: “cash flow diagram”) genoemd. Elke pijl stelt een kasstroom (Engels: “cash flow”) voor die in of uit je kas vloeit. Merk op dat het hier om daadwerkelijke kasstromen gaat in tegenstelling tot bijvoorbeeld boekwaarden welke geen kasstromen zijn. Pijlen naar beneden staan voor kasstromen die uit je kas vloeien, pijlen naar boven staan voor kasstromen die in je kas vloeien.
Dit is een eenvoudige cashflow formule. Eigenlijk is een cashflow formule niet meer dan het optellen van alle geldstromen in een periode, waarbij eventueel de geldwaarde omgerekend wordt voor bijvoorbeeld prijsstijgingen, rendementseisen of breder: prijsfluctuaties. Maar het hoeft niet beperkt te blijven tot geld; een cashflow formule kan ook in bijvoorbeeld kilo citroenen of aantallen vergelijkbare woningen opgesteld worden.
Eindwaarde
De € 110,- die na 1 jaar in je kas stroomt wordt de eindwaarde (Engels: future value) genoemd. Men zegt dan: de eindwaarde van € 100,- bij een jaarlijkse rente van 10% is na 1 jaar € 110,-. Onderstaand figuur is een meer algemene weergave van het voorgaande figuur.
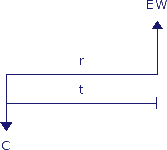
Hierin staat C voor de kasstroom, r voor de rente, t voor de tijdsperiode tussen de twee kasstromen en EW voor de eindwaarde.
Stel dat je de € 110,- na 1 jaar niet opneemt maar nog een jaar laat staan. De bank schrijft dan na dat jaar weer 10% bij over een bedrag van € 110,-. Dit is € 11,- en wordt bijgeschreven bij de € 110,-. Je kunt dan € 121,- opnemen na 2 jaar. Ofwel: de eindwaarde van € 100,- bij een jaarlijkse rente van 10% is na 2 jaar € 121,-. Zie onderstaand figuur.
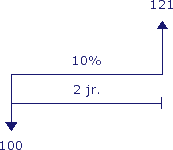
De formule om deze eindwaarde te berekenen:
EW = 100 * (1 + 0,1) * (1 + 0,1) = 100 * (1 + 0,1)2 = 121
Of meer algemeen:
EW = C * ( 1 + r )t
Hierin staat EW voor de eindwaarde, C voor de kasstroom, r voor de jaarlijkse rente en t voor de tijdsperiode tussen de twee kasstromen. De rente is uitgedrukt als perunage (=percentage gedeeld door 100).
Netto eindwaarde en contante waarde
Een begrip dat je ook kunt tegenkomen is de netto eindwaarde (Engels: net future value). Dat is het verschil tussen de eindwaarden van alle kasstromen welke in en uit je kas vloeien. Je vermindert de positieve eindwaarden met de negatieve eindwaarden.
Stel dat je weet dat je over 2 jaar € 121,- moet uitgeven. Welk bedrag moet je nu op de bank zetten om deze uitgave te kunnen dekken wanneer de bank je jaarlijks 10% rente vergoedt?
Het zal je niet verbazen dat je € 100,- op de bank moet zetten om deze uitgave te dekken. Men zegt dan: de contante waarde (Engels: present value) van een kasstroom van € 121,- over 2 jaar bij een rente van 10% is € 100,-.
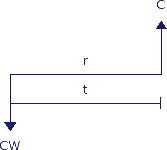
Hierin staat C voor de kasstroom, r voor de rente, t voor de tijdsperiode tussen de twee kasstromen en CW voor de contante waarde.
De formule om deze contante waarde te berekenen:
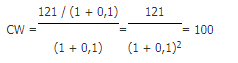
Of algemeen:
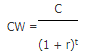
Hierin staat CW voor de contante waarde, C voor de kasstroom, r voor de jaarlijkse rente en t voor de tijdsperiode tussen de twee kasstromen. De rente is uitgedrukt als perunage (=percentage gedeeld door 100).
Netto contante waarde
Een begrip dat je ook zult tegenkomen is de netto contante waarde (Engels: net present value). Dit is niets meer dan het verschil tussen de contante waarden van alle kasstromen welke in en uit je kas vloeien. Je vermindert de positieve contante waarden met de negatieve contante waarden.
Het begrip (netto) contante waarde is een heel belangrijk begrip en zul je vaak tegenkomen. Kasstromen die op verschillende tijdstippen plaatsvinden kun je naar 1 tijdstip contant maken en vervolgens optellen. Dit maakt het mogelijk om te beoordelen of bijvoorbeeld opbrengsten op termijn de kosten van nu kunnen dekken. Een voorbeeld: Je overweegt de cv-ketel in je woning te vervangen door een energiezuiniger ketel en wilt weten of je hier goed aan doet. Je kunt dan de jaarlijkse besparingen stuk voor stuk contant maken. Al deze contante waarden mogen vervolgens bij elkaar worden opgeteld. Wanneer de som van al deze contante waarden hoger is dan de kosten van de nieuwe cv-ketel is de investering verantwoord.
Stel dat je vriend je vraagt hem € 100,- te lenen en hij je belooft je over 2 jaar € 121,- terug te betalen. Je weet ook dat je bank jaarlijks 5% rentevergoeding uitkeert. Waar kies je voor: het geld op de bank zetten of het lenen aan je vriend?
(Intern) Rendement
Omdat de getallen gelijk zijn aan de voorbeeldopgave weet je dat je € 100,- jaarlijks 10% aangroeien als je vriend je na 2 jaar € 121,- terugbetaalt. Dit is beter dan de rentevergoeding van 5% van de bank, dus je doet er beter aan om het geld uit te lenen aan je vriend, mits hij even betrouwbaar is als de bank. De 10% wordt het interne rendement (Engels: internal rate of return) genoemd. Omdat het berekenen van het interne rendement bij sterk wisselende kasstromen niet betrouwbaar is wordt meestal in de vastgoedberekeningen een rendementseis gehanteerd. De eis geeft aan dat het rendement van het vastgoedobject minimaal gelijk moet zijn aan het rendement van een alternatieve belegging zoals bijvoorbeeld een staatslening. Wanneer het vastgoedobject dit rendement niet haalt is het voor de belegger als belegging niet interessant. Vanwege het risico bij een belegging in vastgoed is het gangbaar dat de rendementseis hoger ligt dan rendement op een risicoloze belegging zoals een staatslening.
Geïndexeerde waarde (inflatie)
Wanneer kasstromen niet allemaal op 1 tijdstip plaatsvinden dien je ook rekening te houden met kosten- en opbrengstenstijgingen. Stel dat je over 2 jaar iets wilt aanschaffen dat nu € 114,- kost. Wanneer je rekening houdt met een jaarlijkse prijsstijging van 3% kun je uitrekenen hoeveel het je gaat kosten over 2 jaar. Deze waarde wordt de geïndexeerde waarde genoemd. De algemene kostenstijging wordt meestal aangeduid met de term inflatie. De kosten- en opbrengstenstijgingen kunnen per kasstroomsoort verschillend zijn. Bouwkosten kunnen bijvoorbeeld stijgen met 4% per jaar, terwijl de huuropbrengsten stijgen met 3%. Geïndexeerde waarden worden ook wel aangeduid als nominale waarden omdat dit de werkelijke bedragen voorstellen die in of uit je kas vloeien.
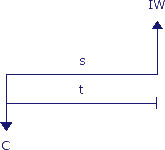
Hierin staat C voor de kasstroom, s voor de stijging, t voor de tijdsperiode tussen de twee kasstromen en IW voor de geïndexeerde waarde.
De formule om deze geïndexeerde waarde te berekenen:
IW = 114 * (1 + 0,03) * (1 + 0,03) = 114 * (1 + 0,03)2 = 121
In algemene termen:
IW = C * (1 + s)t
Hierin staat IW voor de geïndexeerde waarde, C voor de kasstroom, s voor de jaarlijkse stijging en t voor de tijdsperiode tussen de twee kasstromen.
De stijging is uitgedrukt als perunage (=percentage gedeeld door 100).
Prijspeil
De term “prijspeil” wordt gebruikt om aan te geven op welk moment of tijdstip een kosten- of opbrengstenpost van toepassing is. Wanneer je van een gebouw een bouwkostenbegroting laat maken zal deze altijd een prijspeil hebben. Dit betekent dat de prijs geldig is op die datum. Wanneer je het gebouw op een ander tijdstip gaat realiseren zul je de prijs dan ook moeten corrigeren met de prijsstijging (=indexeren).
Stel dat je weet dat je over 2 jaar iets moet aanschaffen dat op dit ogenblik € 114,- kost (prijspeil heden of t=0). Welk bedrag moet je nu op de bank zetten om deze uitgave te kunnen dekken wanneer de bank je jaarlijks 10% rente vergoedt en je verwacht dat de jaarlijkse prijsstijging 3% bedraagt?
In dit geval dien je eerst de aanschafprijs te indexeren naar het jaar waarin de aanschaf plaatsvindt omdat er tweemaal prijsstijging over heen gaat:
IW = 114 * (1 + 0,03)2 = 121
Dit bedrag maak je contant:
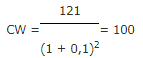
Je dient dus € 100,- op de bank te zetten om deze aanschaf te kunnen doen.
Nominaal of reëel rekenen
De rente die je normaliter ontvangt op je spaarrekening is deels een vergoeding voor uitgestelde consumptie, maar ook deels een vergoeding voor de inflatie (of geldontwaarding). Stel dat de prijzen jaarlijks allemaal 3% stijgen en je inkomen ook jaarlijks 3% stijgt. In essentie blijft je koopkracht dan gelijk omdat je met de 3% extra inkomsten ook inkopen doet die 3% meer kosten. Wanneer je in de berekening de inflatie meeneemt reken je nominaal. Je indexeert bedragen (waar nodig) dan met de inflatie en gebruikt de nominale rente (rente inclusief inflatie) om de contante waarden en eindwaarden uit te rekenen. Je kunt ook de inflatie buiten beschouwing laten. In dat geval reken je reëel. Je dient dan ook de reële rente (rente exclusief inflatie) te gebruiken om de contante waarden en eindwaarden uit te rekenen. In deze blog wordt er nominaal gerekend.
Voorbeeld contante waarde
Op tijdstip t=3 vindt een kasstroom plaats van € 3.000,- (prijspeil t=1) en op tijdstip t=8 vindt een kasstroom plaats van € -6.000,- (prijspeil t=1).
Wat is de totale contante waarde en de totale eindwaarde van beide kasstromen? Ga uit van een nominale rente van 8% en een jaarlijkse kostenstijging (inflatie) van 3%.
Het is een goede gewoonte om altijd het kasstroomdiagram te tekenen:
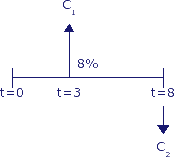
Dit voorbeeld voor rekenen aan kasstromen is op twee manieren uitgewerkt:
- Algebraïsch rekenen aan kasstromen;
- Met een Microsoft Excel spreadsheet rekenen aan kasstromen.
Algebraïsche uitwerking van een kasstroom
De kasstroom van € 3.000,- heeft prijspeil t=1 maar vindt plaats op t=3. Dit bedrag moet eerst worden voor 2 jaar worden geïndexeerd met 3% stijging per jaar. Hiervoor gebruiken we de algemene formule voor het bepalen van de geïndexeerde waarde:
IW = C * (1 + s)t
Wanneer de gegevens in deze formule worden ingevoerd:
IW = 3.000 * (1 + 0,03)2 = 31.83
Vervolgens bereken je de contante waarde. Berekend met de algemene formule voor het bepalen van de contante waarde:
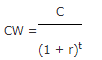
Ingevuld in de formule:
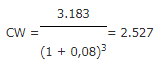
Voor de berekening van de contante waarde van de kasstroom van € -6.000,- worden de formules voor het indexeren en het contant maken tot 1 formule samengevoegd:
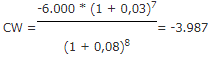
De beide contante waarden mogen bij elkaar worden opgeteld:
NCW = 2.527 - 3.987 = -1.460
De netto contante waarde is dus € -1.460.
Voor de berekening van de eindwaarde moet het bedrag van € 3.000,- ook eerst worden geïndexeerd.
IW = 3.000 * (1 + 0,03)2 = 3.183
Vervolgens wordt de eindwaarde berekend via de algemene formule voor het bepalen van de eindwaarde:
EW = C * (1 + r)t
Ingevuld in de formule:
EW = 3.183 * (1 + 0,08)5 = 4.676
De kasstroom van € -6.000,- vindt plaats op t=8 en dit is hetzelfde moment waarop de eindwaarde wordt bepaald voor de Netto Contante Waarde. Dit betekent dat de eindwaarde van deze kasstroom gelijk is aan de geïndexeerde waarde (hetzelfde geldt voor de netto contante waarde van een kasstroom die op t=0 plaatsvindt):
EW = -6.000 * (1 + 0,03)7 = -7.379
De beide eindwaarden mogen bij elkaar worden opgeteld:
NEW = 4.676 - 7.379 = -2.703
De netto eindwaarde is dus € -2.703,-.
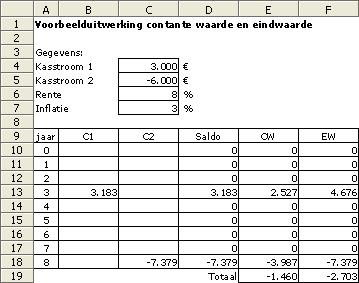
Netto contante waarde uitwerken met Excel
In de afbeelding hieronder kun je zien hoe de uitwerking met behulp van een spreadsheet programma eruit zou kunnen zien. Het is verstandig om alle unieke gegevens in unieke cellen in te vullen. Vervolgens verwijs je in de berekeningen naar deze unieke cellen. Dit is in dit voorbeeld te zien in het lijstje met gegevens. De meest belangrijke formules in deze spreadsheet worden stuk voor stuk hieronder behandeld.
Een voorbeeld van een liquiditeitsbegroting met Excel en Exact Online is te vinden in het artikel Excel liquiditeitsbegroting voor Exact Online (cash flow met consolidatie).
| Cel | Excel-formule | Toelichting |
|---|---|---|
| B13 | =C4*(1+C7/100)^2 |
In deze cel wordt de kasstroom van € 3.000,- geïndexeerd. Omdat dit bedrag prijspeil t=1 heeft wordt het bedrag 2 jaar geïndexeerd met 3% per jaar |
| C18 | =C5*(1+C7/100)^7 |
In deze cel wordt de kasstroom van € -6.000,- geïndexeerd. Omdat dit bedrag prijspeil t=1 heeft wordt het bedrag 7 jaar geïndexeerd met 3% per jaar |
| D10 | =SUM(B10:C10) |
In deze cel wordt het jaarsaldo berekend. Deze formule is gekopieerd tot en met cel D18. |
| E10 | =D10/(1+$C$6/100)^A10 |
In deze cel wordt het jaarsaldo contant gemaakt. Het vereiste rendement wordt gebruikt en de uitkomst is afhankelijk van het jaar waarin de kasstroom plaatsvindt. De verwijzing naar het rendement is absoluut gemaakt via de dollartekens. Deze formule is gekopieerd tot en met cel E18. |
| E19 | =SUM(E10:E18) |
Deze cel geeft de netto contante waarde weer. |
| F10 | =D10*(1+$C$6/100)^(8-A10) |
In deze cel wordt de eindwaarde van het jaarsaldo berekend. Het vereiste rendement wordt gebruikt en de uitkomst is afhankelijk van het jaar waarin de kasstroom plaatsvindt. Het jaar van de kasstroom wordt in mindering gebracht op het tijdstip van de laatste kasstroom (t=8). Deze formule is gekopieerd tot en met cel F18. |
| F19 | =SUM(F10:F18) |
Deze cel geeft de netto eindwaarde weer |
Tot slot
Ik hoop dat je met deze korte introductie in de financiële rekenkunde je projecten beter kunt waarderen op hun merites. Heb je nog vragen? Laat hieronder een reactie achter, dan zullen wij deze vragen beantwoorden.